对用户来说,一般买卖的隐私维护(译者注:文中有时也会简称为隐私买卖)基本上算是一个已处理了的问题(虽然在研究上依然遗留了一些应战)。假如咱们想在不泄漏账户余额或转账金额的前提下搬运密码学钱银,咱们有诸如大零币(Zcash)或门罗币(Monero)这样可承受的选项。不过,关于去中心化运用或许智能合约来说,隐私维护仍是一个没有处理的问题。
是什么让智能合约与一般买卖在输入/输出(I/O)的隐私维护上有所不同呢?
在本文中,咱们将解密隐私维护从一般买卖拓宽到智能合约上会遇到哪些应战。为此,咱们将调查运用于隐私币的常用密码学东西,并探讨为什么这些东西不太合适更杂乱的隐私运用。最终,咱们将简要介绍最近提出的一些智能合约隐私维护计划。
隐私维护的界说
“隐私维护” 到底是什么意思?
咱们将从函数的角度来界说隐私维护。例如,咱们能够把 买卖 看作是一些函数,它以账户余额和转账金额作为输入。然后它输出更新后的余额。

图 1:以函数来表明买卖进程。
(要实现隐私维护)咱们能够考虑躲藏函数的输入和输出。就买卖而言,这能够让咱们躲藏账户余额和转账金额。你会愿意揭露你的账户余额和转账历史吗?或许不会吧。因而,咱们至少要支撑函数(以及随后的智能合约)的 I/O 隐私维护。

图 2:躲藏函数的 I/O。
咱们也能够考虑躲藏函数的调用者信息。有时候,函数输入会留下关于函数调用者身份的线索。在实践中,躲藏函数的输入和输出通常会和躲藏函数调用者的身份相结合。

图 3:躲藏函数调用者。
最终,咱们能够考虑躲藏函数自身。这在密码学钱银范畴不太常见,其通常与躲藏函数的输入/输出相结合。

图 4:躲藏函数自身。
当你在本文中看到 “隐私维护” 这个词时,请把它当成一个总称,指的是 至少支撑 I/O 隐私维护 的东西。
好吧,但咱们要在哪里用到隐私维护呢?
咱们能够以为一般买卖的隐私维护已被处理(至少在可行性方面确实如此,可扩展性又是另一回事了),所以让咱们直接转到智能合约的隐私维护。
不过,咱们先绕个弯子,回顾一下以太坊 ……
以太坊支撑用户自界说的合约,合约以代码的方式履行(也便是 “智能合约”)。这些合约用以太坊自己的图灵齐备的语言编写,每履行一个操作都要付出一些(预设的)费用。因而,每笔买卖都要附上买卖费,以激励矿工打包买卖。
运用的隐私维护
智能合约让咱们在区块链上得以构建丰厚的运用 —— 从用户可买卖各种密码学钱银及其衍生品的去中心化买卖所(DEX),到答应权益持有者对提案进行投票的去中心化自治组织(DAO)。
我觉得没必要长篇大论讲解为什么 DAO 需求隐私维护;在现实生活中,投票通常都是私下进行的,所以想要躲藏咱们的虚拟投票也是非常合理的。
另一方面,去中心化买卖所的隐私维护需求解说一下。抢先买卖(front-running)无论是对中心化买卖所仍是去中心化买卖所都是一个问题。在区块链世界里,抢先买卖者亲近观察已提交的订单,并经过付出更高的买卖费(贿赂矿工)实现插队。这使得抢先买卖者 Eve 能够抢在 Bob 之前买到 Bob 想买的证券,并随后以更高的价格卖给 Bob。封闭式拍卖是处理这个问题的一个或许的方法。关于有爱好的读者,能够在这里找到更多关于在去中心化买卖所的抢先买卖的信息。
不过,以太坊的智能合约并没有供给任何方式的开箱即用的隐私维护。一切的信息都是揭露可检查的 —— 合约的输入/输出,合约的功能,参与的用户,等等。为以太坊的智能合约 添加 隐私维护不是一件简略的事情,由于以太坊从一开端就没有被规划成支撑隐私维护。虽然在以太坊上能够实现隐私买卖(经过 1,2),可是更杂乱的隐私维护操作往往过于昂贵,乃至超过以太坊单个区块的费用限额(即 gas limit),以至于无法实现。
难道咱们就不能规划一种新的密码学钱银,从一开端就支撑任何函数的隐私维护吗?毕竟,大零币和门罗币便是这样做的。
现在咱们还不清楚如何在密码学钱银中支撑恣意函数(例如在投票和买卖所中需求的函数)的 I/O 隐私维护。为了理解这些应战,咱们需求调查密码学钱银是如何支撑隐私买卖的。
通往隐私维护之路
咱们先调查用于一般买卖 I/O 隐私维护的密码学东西。咱们将重视账户模型而非 UTXO 模型的加密钱银。账户模型在支撑智能合约的场景下特别有用,不过账户模型关于隐私核算来说不是有必要的(咱们将在后面看到)。
东西 1:同态加法
大多数密码学钱银的隐私维护计划都依赖于具有 加法同态 的加密或许诺计划。为了简略起见,咱们将专心于加密计划,但相同的准则也适用于许诺计划。
在加法同态加密计划下,咱们有以下等式:Enc(a) + Enc(b) = Enc(a + b)。
因而,加法同态加密计划答应任何人 这样验证买卖的有用性:Enc(balance) + Enc(transfer amount) = Enc(balance + transfer amount) (余额的加密值与转账额的加密值之和,恰等于两者之和的加密值)。
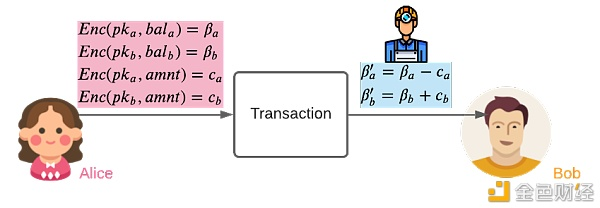
图 5:Alice 在不泄漏账户余额或转账金额的情况下转账。
Alice 有自己的的公钥 —— pk_a。她用自己的公钥加密账户余额 bal_a(这样就只需她自己知道账户余额)。咱们用 β_a 表明她加密后的余额,β_a = Enc(pk_a, bal_a)。Alice 的公钥 pk_a 和加密后的余额 β_a 都揭露在网上,任何人都能检查。
Bob 相同如此;他也有自己的公钥 pk_b,只需他自己知道的账户余额 bal_b,以及用他的公钥加密后的余额 β_b,β_b = Enc(pk_b, bal_b)。
假如 Alice 想在不泄漏转账金额(amnt)或她自己的账户余额的情况下向 Bob 转账,她只需求发布用她自己的公钥加密后的转账金额,以及用 Bob 的公钥加密后的转账金额。咱们别离用 c_a = Enc(pk_a, amnt) 和 c_b = Enc(pk_b, amnt) 来表明这些值。
现在任何人都能够核算更新后的余额。Alice 更新后的账户余额是 β_a - c_a,Bob 更新后的账户余额是 β_b + c_b。
等一下!假如一切这些值都被加密了,咱们怎样知道 Alice 的账户里有没有足够的钱付出 amnt 金额的转账呢?咱们又怎样知道 c_a 和 c_b 加密的金额是不是一样的呢?
这就要用到咱们的下一个东西 —— 零常识证明了。
东西 2:零常识证明(ZKP)
为了保证 Alice 没有在上述买卖中做弊,她需求在买卖中附上一个证明。这个证明需求表明她的账上有足够的资金以完结买卖,她没有向 Bob 转一笔负数的金额(无论是意外仍是恶意),并且 c_a 和 c_b 确实加密了相同的金额。
当然,Alice 不想泄漏她真实的账户余额和转账金额;因而,她附上了一个零常识证明 π,让一切其他用户信赖必要的条件现已被满意,而无需泄漏任何额定的信息(如她的账户余额或转账金额)。
现在把一切的东西放在一同 ...

图 6:现在给隐私买卖附上必要的 ZKP
Alice 用她和 Bob 的公钥别离对转账金额进行加密,得到了 c_a 和 c_b。她供给了一个 ZKP,π,证明她在买卖中没有做弊。矿工们会验证一切的必要条件是否被满意,ZKP 是否有用。然后,他们会运用同态加法别离更新 Alice 和 Bob 的加密余额:β_a = β_a - c_a,β_b = β_b + c_b。留意,虽然用户供给了加密后的输入和一个 ZKP,可是矿工需求负责履行核算以及更新加密后的余额。在区块链中,咱们假定大多数矿工是诚笃的,所以咱们知道他们会正确地更新 Alice 和 Bob 的余额。
注:这是一个大大简化的解说(例如,省去了为保证加密安全所需求的随机性)
将一般买卖的隐私维护技能拓宽到智能合约上面对的应战
所以咱们刚刚现已看到了,咱们能够履行躲藏输入和输出的买卖。那么咱们能够把在隐私买卖中用到的技能,用于支撑运用的 I/O 隐私维护吗?换句话说:
隐私核算和隐私买卖是否不同?假如是,为什么?
问题 1
需求留意的是,隐私买卖需求满意设定的条件才是正确的(即发送方要有足够的资金,转账金额有必要为正数,等等)。咱们如何能弄清楚一个恣意的合约需求满意哪些条件?这些条件显然受特定的运用影响。在投票中,咱们或许期望证明咱们躲藏的投票是在正确的范围内进行的,而关于拍卖,咱们或许期望证明咱们的账上有足够的资金用于封闭投标。
对问题 1 的潜在处理计划
这个问题也没那么严重;只是需求用户做更多的作业。去中心化运用的开发者有必要清晰他们的特定运用需求满意哪些条件,并将这些条件传达给用户。为了能够证明各式各样的条件,咱们或许期望在计划中支撑一些通用的 ZKP。所谓 通用 的 ZKP 便是能够证明恣意的声明(不像那些现在用在大零币里的 ZKP,它们是非通用的)。
问题 2
在一般买卖中,咱们只对属于同一个用户的值进行操作(即运用同一个密钥加密)。比方在图 6 中,矿工把用 Alice 的公钥加密后的余额与用 Alice 的公钥加密后的转账金额相加。假如咱们想对属于不同用户的输入值进行隐私核算呢?这并不是一个多么勉强的需求,比方咱们考虑对投票做隐私维护时就会触及。
对问题 2 的潜在处理计划
现在还不清楚如何在用户相互之间不泄漏输入明文的情况下,支撑对不同用户的输入进行核算。有一些先进的密码学元件(比方安全多方核算和根据多密钥的全同态加密 FHE),答运用户对不同密钥加密的输入进行核算。可是,这些计划的本钱都非常高,并且有许多缺点。在密码学钱银的运用场景下,现在好像没有人有一个很好的处理计划来处理这个问题(除了与参与核算的其他用户共享明文,然后在同一个密钥下加密)。
问题 3
一般买卖只需求同态加法,由于咱们只需求将加密的转账金额加到加密的余额上。假如咱们想进行更杂乱的核算,或许触及到乘法呢?
对问题 3 的潜在处理计划
同态乘法答应咱们将加密的输入相乘,使得 Enc(a) * Enc(b) = Enc(a * b) 。经过同态加法和同态乘法,咱们能够表明恣意多项式函数。所以,咱们很自然地想到这个问题:
咱们能够支撑同态乘法吗?
一个既能支撑同态加法,又能支撑同态乘法的加密计划是全同态加密(FHE)。运用 FHE,咱们依然能够遵从图 6 中所描绘的模型。也便是,用户指定加密输入,要运行的函数,以及证明加密输入满意必要条件的 ZKP。矿工能够验证 ZKP。他们运用同态加法和同态乘法直接对用户供给的密文进行操作。
不幸的是,FHE 计划运用根据格(lattice)的加密技能,这(在现在)与密码学钱银中运用的超高效的 ZKP 并不兼容。咱们从前写过关于 FHE 及其问题的文章。现在,由于 FHE 存在一些缺点,还没有人提出根据 FHE 的处理计划。
这样,咱们现在就只剩余两种方法来处理问题 3 了。
-
承受咱们只能支撑同态加法的现状,遵从隐私买卖模型。

图 7:遵从隐私买卖模型
在这里,用户供给加密后的输入和一个 ZKP,证明他们的输入满意特定运用的一些指定条件。矿工验证证明,运用同态加法对输入进行操作。需求留意,运用于输入的函数只能用加法来表明。因而,只需函数只需求用到同态加法,咱们就能够要求矿工对咱们加密的输入履行恣意满意该条件的函数。这便是 Zether 所选用的方法。
-
要求用户线下核算。这样咱们就不需求为加密/许诺支撑同态乘法了。
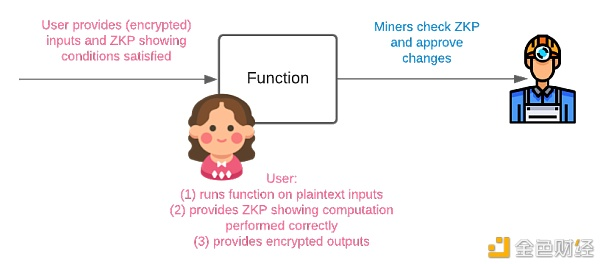
图 8:将作业外包给用户
在这里,咱们要求用户 Alice 将对明文的几乎一切核算都放到线下进行。她会发布核算的加密输入和加密输出。由于核算是在线下完结的(因而咱们并不知道 Alice 是否诚笃),她相同需求供给一个 ZKP 证明核算进程是正确的。留意,这一步对隐私买卖来说是不必要的,由于矿工会履行核算,而咱们假定大多数矿工是诚笃的。就运用而言,她或许还需求另一个 ZKP,证明运用指定的条件已被满意。矿工所需求做的便是验证 ZKP 是否有用,然后同意 Alice 提出的状态变更。这便是 Zexe 和 Zkay 所采纳的方法。
我不会在这里讨论哪种方法(图 7 与图 8)更优;只想阐明它们是不同 的。
智能合约的隐私维护
前面咱们现已谈到了在区块链中支撑恣意函数的隐私维护要面对的一些问题,现在让咱们来看一看一些已有计划的结构。
假如前面说得还不行清楚,我再重申一下,这个范畴距离处理问题还有很长的路要走。规划这些结构的论文(即 Zether,Zkay,Zexe)都是在曩昔两年中宣布的。
Zether 是一个建立在以太坊上的隐私买卖计划。它能够延伸到支撑有限的智能合约的 I/O 隐私维护 —— 即那些能够经过同态加法表明的合约。这使得咱们能够履行简略的封闭式拍卖(假定竞拍者会一次买下一切单位)和隐私投票(假定投票选项非 0 即 1)。惋惜的是,由于 gas 的限制,现在在以太坊上只能实现在买卖中躲藏用户余额和转账金额。与接下来的两种结构不同,Zether 运用的是 “通明” 的 ZKP(即 ZKP 不需求可信的发动设置)。
Zkay 相同延伸了以太坊的规划以支撑智能合约的隐私维护。他们依赖 ZKP 保障隐私核算的正确性,然后能够将大部分作业丢给用户在线下完结。因而,这种规划选择使得它们能够支撑比 Zether 更多类型的函数。
Zexe 则试图延展大零币的规划,以支撑恣意脚本。与前两者不同,Zexe 还能够支撑函数自身的隐私维护。
| 计划 | 隐私维护类型 | 模型 | 表达能力 | 根据哪条链规划 |
|---|---|---|---|---|
| Zether | I/O | 图 7 | 加法函数 | 以太坊 |
| Zkay* | I/O | 图 8 | 恣意函数 | 以太坊 |
| Zexe* | I/O, 函数** | 图 8 | 恣意函数 | 大零币 |
Zkay 和 Zexe(如前所述)运用的是带有可信设置的 ZKP 计划。不过,这些 ZKP 计划当然能够被不需求可信设置的计划替代。
** 在区块链的场景中,I/O 隐私维护好像比函数隐私维护更有意义,由于用户很或许期望在决议是否参与合约之前先对合约进行审计。
请留意,还有其他一些用于智能合约隐私维护的结构(即 Ekiden、Hawk、Arbitrum),可是这些计划都需求某种准-受信赖(semi-trusted)的管理器或受信赖的硬件。
大多数智能合约的隐私维护计划都需求额定的安全假定 —— 无论是受信赖的发动设置(trusted setup),准-受信赖的管理器仍是受信赖的硬件。可是,ZKP 是一个快速发展的范畴,更高效通明的结构很或许会被发明出来。
期许
当触及表达能力,信赖和功率时,在智能合约的隐私维护上进行的探索提出了许多风趣的理论和实践应战。现在,很难说在图 7 或许图 8 所代表的方法中,哪种(假如有一种的话)或许会在区块链的隐私核算中胜出。此外,未来全同态加密的发展能否转化到区块链中以处理问题 3,这也是一个很风趣的看点。
视野开拓
从某种意义上来说,公司制度就是民主制在企业中的应用。股东就是选民,董事会就是企业中的议会,CEO对应着行政领导人,监事会则是司法机构的缩影。 战略被定义为“企业长期基本目标的决定,以及为贯彻这些目标所必需采纳的行动方针和资源分配”。结构则被定义为“为管理一个企业所采用的组织设计”。 《战略与结构》一书的中心论点可以概括为:一个企业面对新的机会(进入相关的产品市场和地理扩张)可能会采取一个投资战略;但这个投资战略就生产工艺、产品和地理来说目标越是远大,发展出一个能够协调投入流量和产出分配的管理结构就越是关键;因为只有这种相应的结构才能协调多样化和复杂化的企业生产过程,从而证明大规模投资的合理性。 战略起源于对机会和需求的考量,来自于不断变化的人口、收入和技术的识别,以便更有利可图地利用现有的或新增的资源。新的战略要求建立新的或至少更新了的结构,才能使扩大了的企业更有效地运营。-《战略与结构》




