以 Uniswap 为代表的稳定乘积 AMM 在加密财物商场取得了巨大成功，但也受无常丢失之累。一些项目试图在 Uniswap 的基础上进行改善，比方引进预言机报价来下降无常丢失，但没有有公认的成功改善计划。
要更好地了解这些问题，需求回到 AMM 的一般理论：1. 除了稳定乘积公式以外，还能采取其他数学函数吗，这些数学函数应该满意哪些要求？2. 在其他数学函数下，也会有无常丢失吗？3. 什么样的数学函数是最佳的？4. AMM 与加密财物商场的其他买卖方式的中心区别是什么？
本文试图答复这些问题，共分三部分：榜首部分评论 AMM 的一般方式，第二部分评论 AMM 的若干特殊方式，第三部分比较 AMM 与加密财物商场的其他买卖方式。
AMM 的一般方式
为剖析的简略，本文只研讨针对两种加密财物的 AMM，但相关研讨很容易拓宽到三种或三种以上加密财物的情形。
考虑两种加密财物，分别称为 X 和 Y ，并以加密财物 X 为记账单位，也便是一切价格、市值的单位均为加密财物 X 。AMM 的状况体现为流动性池中两种加密财物的数量，假设在某一时刻为 (x,y)。在 AMM 的一般方式下，不论两种加密财物之间怎么买卖（不考虑买卖手续费的影响，下同），流动性池始终满意
在流动性池状况为 (x,y) 时，流动性池中两种加密财物的市值之间的联系为
(1) 和 (7) 从不同视点刻画了 AMM，它们之间是相互等价的。换言之，经过限制流动性池中两种加密财物的市值之间的函数联系，也能定义 AMM。
(8) 虽然是一个简略剖析，但对了解加密财物市值有丰富含义。榜首，即便在加密财物数量不变的情况下，它们之间的买卖会改变它们之间的价格联系，然后使加密财物总市值发生变化。
总的来说，这一部分对 AMM 的一般方式的剖析首要得到如下结论：
AMM 的若干特殊方式
依据榜首部分的评论，任何单调递减凸函数均能够用来定义 AMM。
为便利与 Uniswap 的比较，接下来运用一个等价表述
(16) 阐明，在其他条件相同的情况下，α 越大，无常丢失的数值越小。这一点也经过对 (15) 的数值核算验证（表 1）：
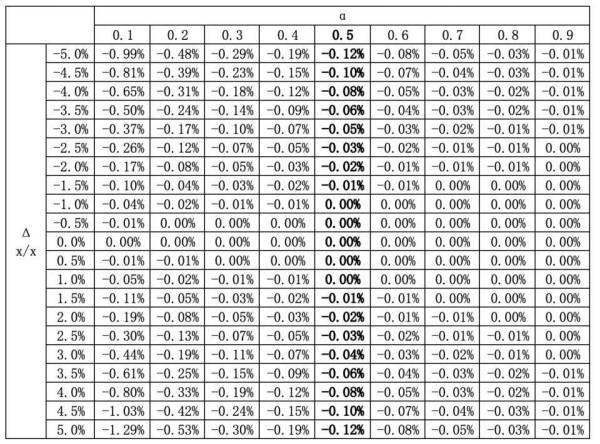表 1：α对无常丢失的影响
假如让 α取值为 1/2，就得到 Uniswap 的稳定乘积公式，因此 Uniswap 属于一类广义 AMM 的特例。因为没有任何一对加密财物在基本面上（比方市值、流动性和用户数等）完全相同，所以α=1/2 没有逻辑上的必定性。假如要下降无常丢失，能够适当调高α 。比方，假如加密财物 X 是稳定币，加密财物 Y 是以太币，α 完全能够大于 1/2，一个选项是α=2/3 。在一般情况下， α能够经过 AMM 社区自治决议。
AMM 与其他买卖方式的比较
(2) 能够等价表述为
引进如下函数
总的来说，AMM 的中心机制是：流动性提供者基于算法承诺，为投资者提供关于买卖价格和数量的确认性。这种确认性的代价是流动性提供者锁定流动性并承当无常丢失。
为更好了解这一点，需求将 AMM 与拍卖机制相比较。在加密财物商场的各种买卖机制中，只需存在订单薄，不论有没有做市商，其中心都是拍卖机制。接下来以 Algorand 采取的荷兰式拍卖为例阐明。虽然这个比如是出售财物，前文对 AMM 的剖析是从购买财物的视点进行，但不同视角不影响剖析逻辑。
荷兰式拍卖也被称为「减价式拍卖」：卖方由高往低喊价，直到有人乐意购买，此价即为成交价。在战略上能够证明，荷兰式拍卖等价于榜首价格封闭式拍卖。在榜首价格封闭式拍卖中，一切竞拍者一起提交「暗标」（sealed bids），然后没有竞拍者知道其他竞拍者的出价。出价最高的竞拍者取得标的，并付出他的出价。
Algorand 的荷兰式拍卖与美国国债一级商场拍卖相似。美国国债一级商场采用荷兰式拍卖有相当长历史。从 1929 年-1992 年，美国财政部运用「多重价格」荷兰式拍卖。榜首步：一级买卖商提交自己能承受的到期收益率及在该到期收益率上乐意购买的数量。第二步：一切竞标将按到期收益率从低到高摆放（对应着债券购买价格从高到低摆放），直到意愿购买数量等于债券的供给数量，临界到期收益率即为清算价（clearing price）。第三步：一切提交的到期收益率低于清算价的一级买卖商按自己乐意购买的数量取得债券，购买价格依据各自的到期收益率核算。临界到期收益率上的一级买卖商按各自乐意购买的数量分配剩余额度。因此，在竞标中胜出的一级买卖商购买债券的价格是不相同的。
1992 年至今，美国财政部改用「单一价格」荷兰式拍卖。「单一价格」荷兰式的拍卖的前两步与「多重价格」荷兰式拍卖相同。在第三步，仍是一切提交的到期收益率低于清算价的一级买卖商按自己乐意购买的数量取得债券，但购买价格依据清算价核算。「单一价格」荷兰式拍卖中引进了两类竞标：榜首种是竞争性的，即竞标者要一起阐明自己能承受的到期收益率及在该到期收益率上乐意购买的数量；第二种对错竞争性的，即竞标者只需阐明自己乐意购买的数量。在存在两类竞标的情况下，清算价的确认办法同上。但在债券额度分配上引进优先顺序：先满意非竞争性竞标，再将剩余额度分配给竞争性竞标，按提交的到期收益率从低到高分配。
Algorand 的荷兰式拍卖相当于「单一价格」+竞争性竞标。榜首步：确认 Algo 拍卖数量以及开始竞拍价格；第二步：竞拍价格按时间线性递减（图 1），在每个竞拍价格上记载竞拍者乐意购买的数量，直到累计的乐意购买数量等于拍卖数量，临界价格即为清算价（图 2）；第三步：竞拍价格高于清算价的竞拍者胜出，按竞拍价格从高到低分配 Algo 额度，价格一致为清算价。
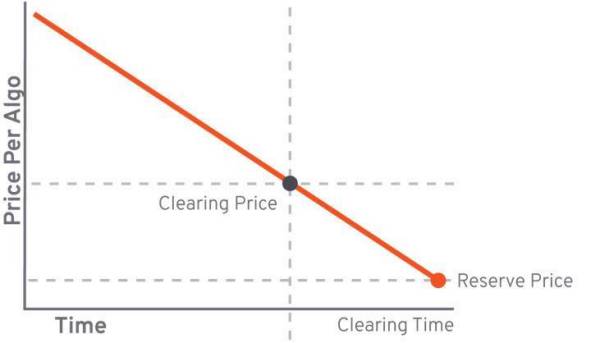图 1：Algo 竞拍价随时间线性递减
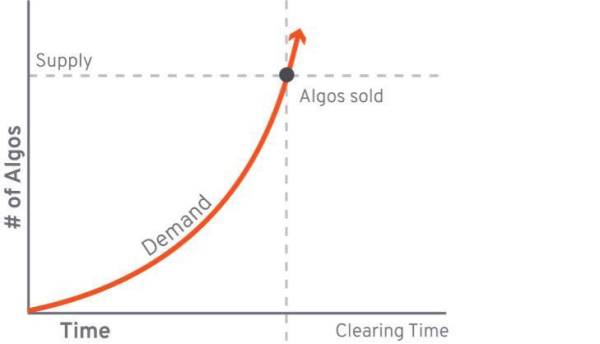图 2：Aglo 清算价的确认
从荷兰式拍卖实践不难看出，买卖价格和数量由商场决议，在事前看是高度不确认性的，而 AMM 能提供这方面的确认性。对 AMM 与场内会集促成、场外询价成交等买卖机制的区别，也能够按相似逻辑了解。
视野开拓
短缺与缺乏不同，缺乏是指某物品的需求使价格或代价高于零。-《经济解释（二〇一四合订本）》
